K-Means Clustering

What is K-Means Clustering?

K-Means Clustering is performed by updating the centroid based on the distance between the centroid and each data point.

Steps

---

• Step 1
  Choose the number $K$ of clusters. Let’s assume that $K$ is 2, and see the data set.
  

• Step 2
  Select $K$ points at random, the centroids. The $K$ points can be actual points in the data set or they can be just random points.
  

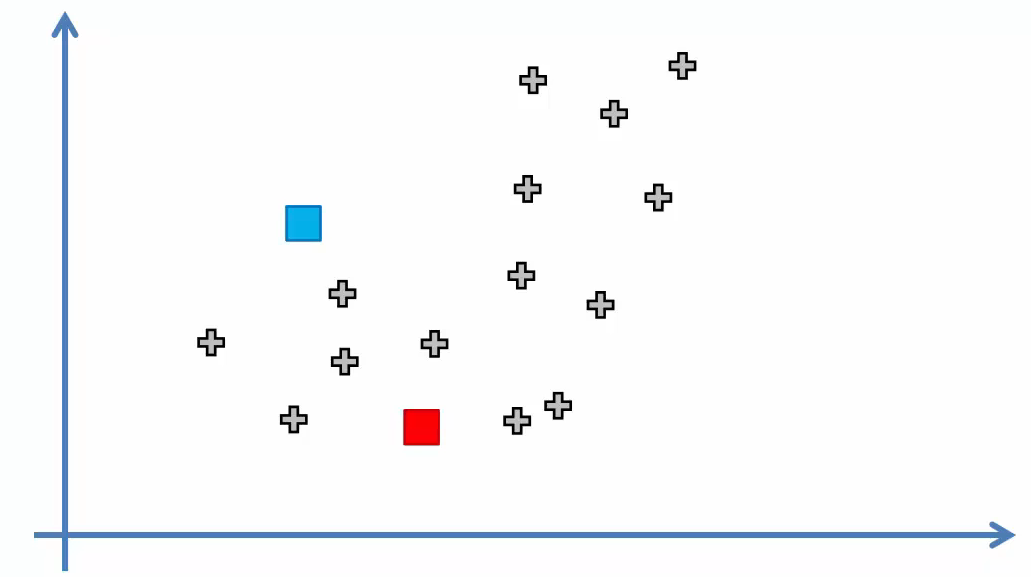
• Step 3
  Assign each data point to the closest centroid. This step forms $K$ clusters
  

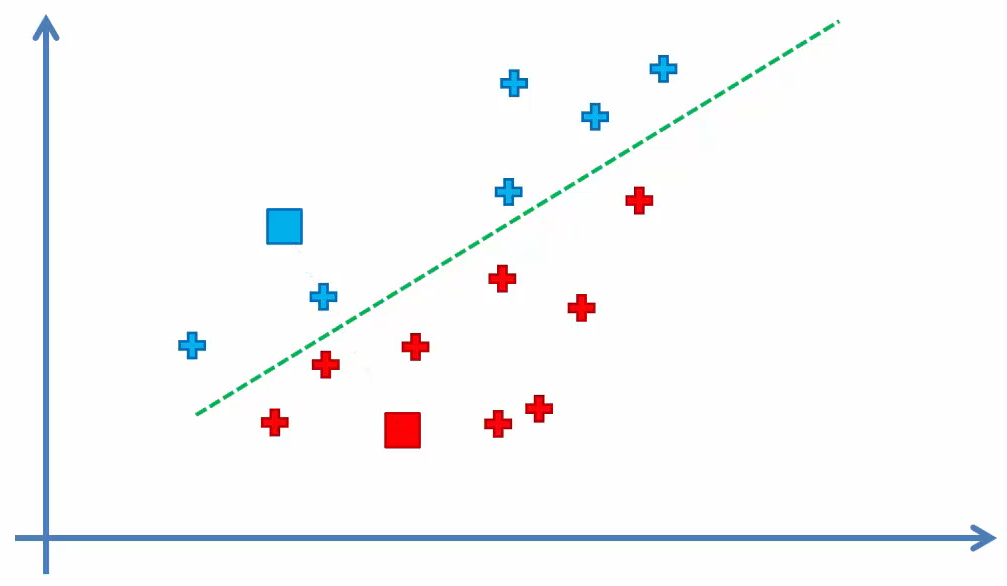
• Step 4
  Compute and place the new centroid of each cluster. In other words, move the centroids to the center of each cluster.
  

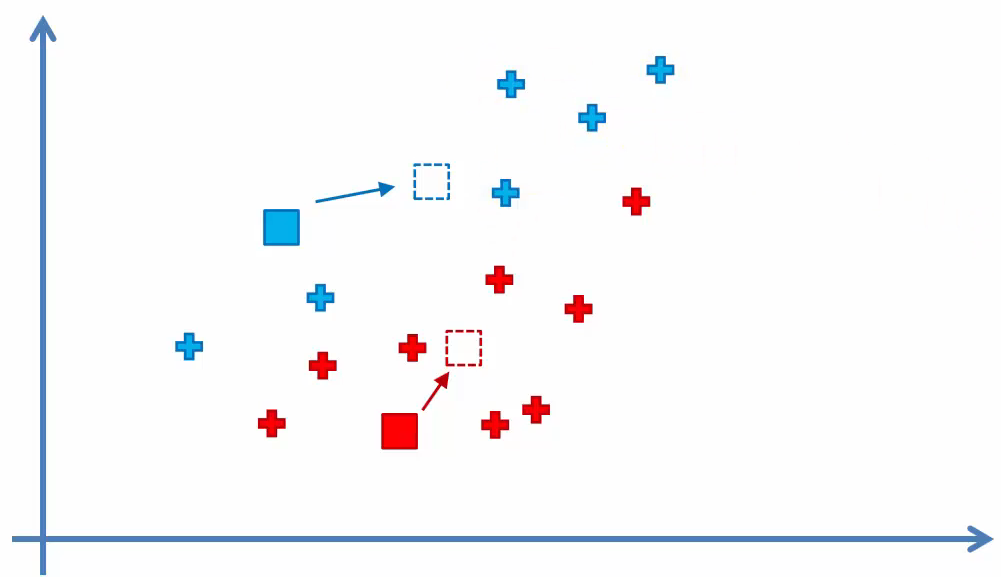
• Step 5
  Reassign each data point to the new closest centroid.
  If any reassignment took place, go to Step 4, otherwise K-Means Clustering is done.
  

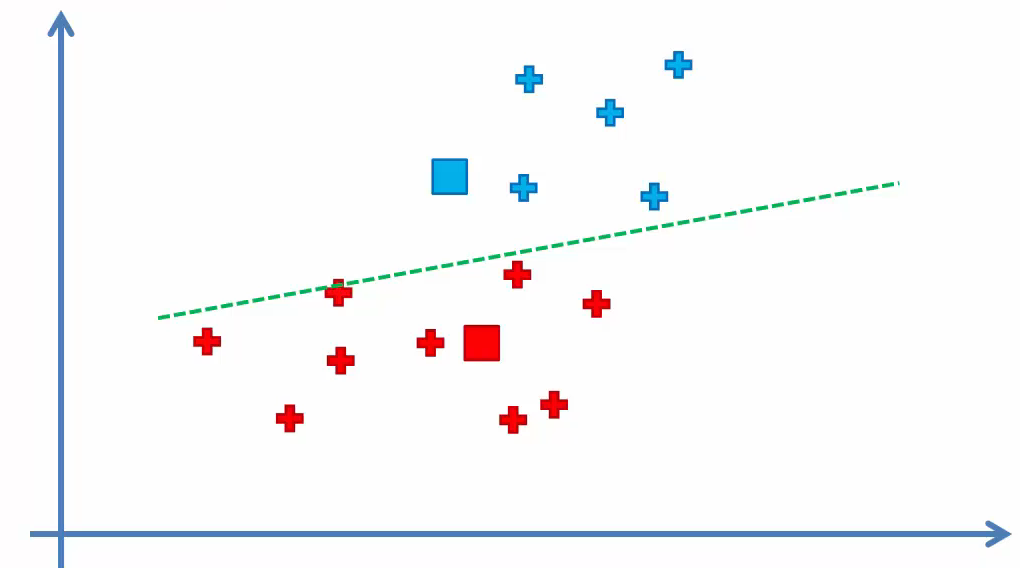
Repeat step 4 as the clusters of some points have changed.


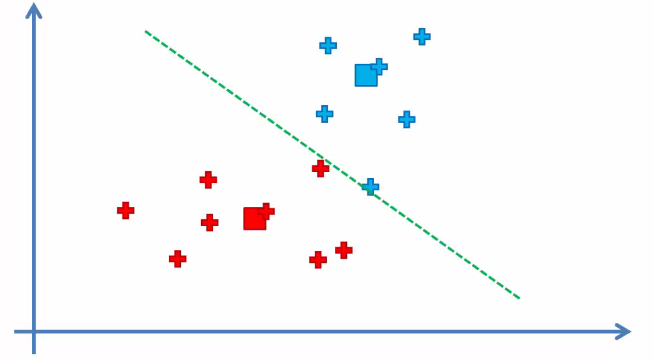
Repeat step 4 as the clusters of some points have changed.


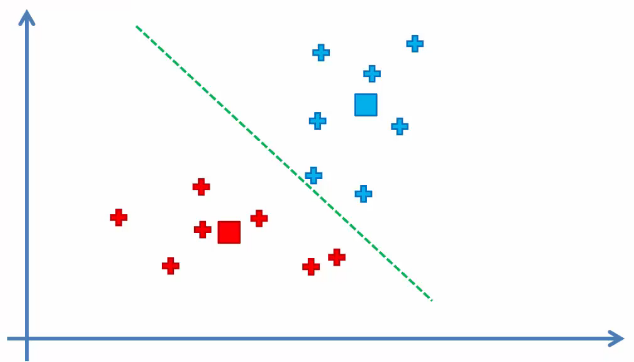
Repeat step 4 as the clusters of some points have changed.


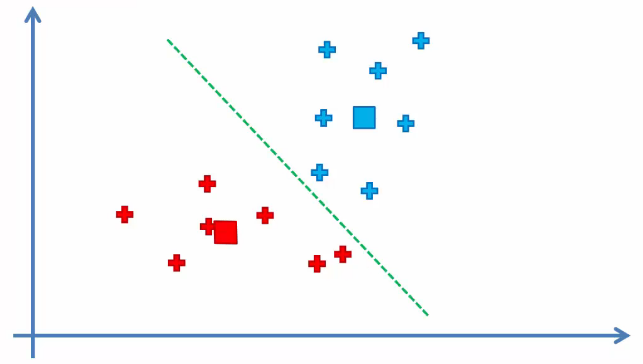
Clustering is done because nothing has changed.

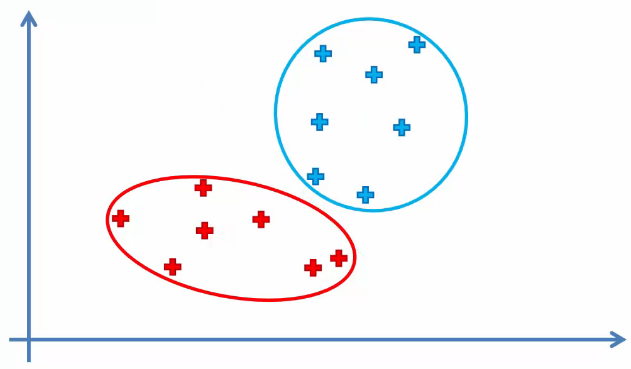
The K-Means Random Initialization Trap

---

The K-Means random initialization trap is that the result can be different from what is expected.

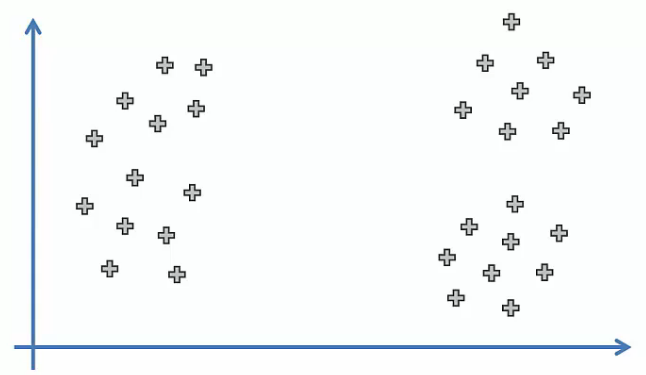
How are clusters created in this dataset when $K=3$?

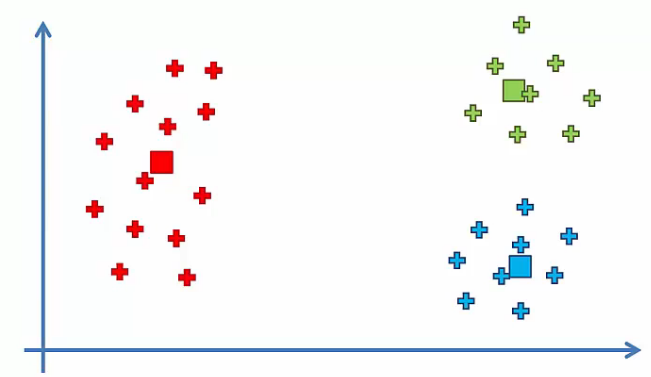
Clustering like image above would be ideal. However, as we mentioned in Step 2, the centroid can be initialized randomly. Then, if centroids are initialized like image below, is there any difference between what expected?

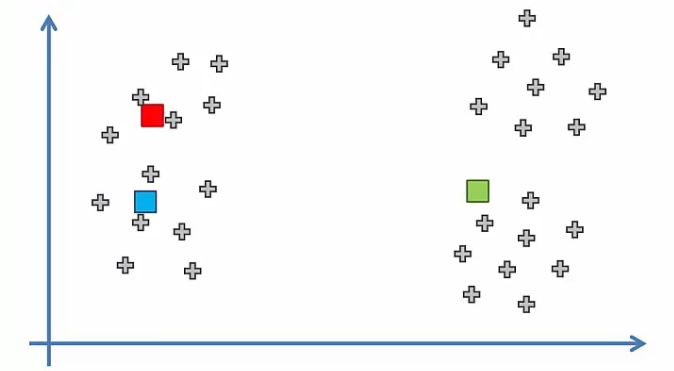
The answer is yes. As you can see in the image below, the result is somewhat different from we expected.

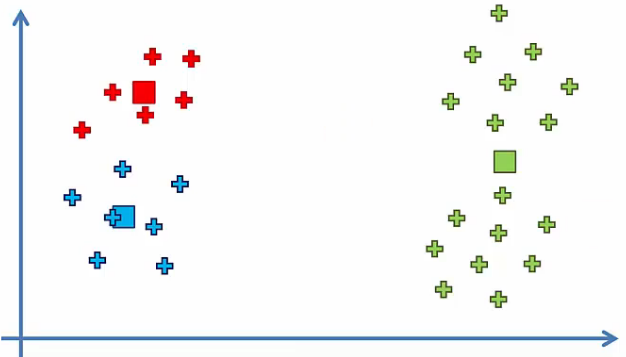
To solve this problem, K-Means++ exists, but it can still happen. So, it would be good idea to be aware of this issue.

How to choose the ideal numbers of $K$?

---

We can choose $K$ using WCSS:

$ WCSS = \displaystyle\sum_{P_{i} \in Cluster 1}^{}{distance(P_{i},C{1})^2} + \displaystyle\sum_{P_{i} \in Cluster 2}^{}{distance(P_{i},C{2})^2} + \ldots + \displaystyle\sum_{P_{i} \in Cluster n}^{}{distance(P_{i},C{n})^2}$

The lower the value of WCSS, the more sophisticated the performance. Also, the lower value of WCSS, the longer the execution time.

Then, how to choose $K$? What I recommend is to choose a value for $K$ when there is no more significant change in WCSS value in the graph anymore.

Look at this graph:

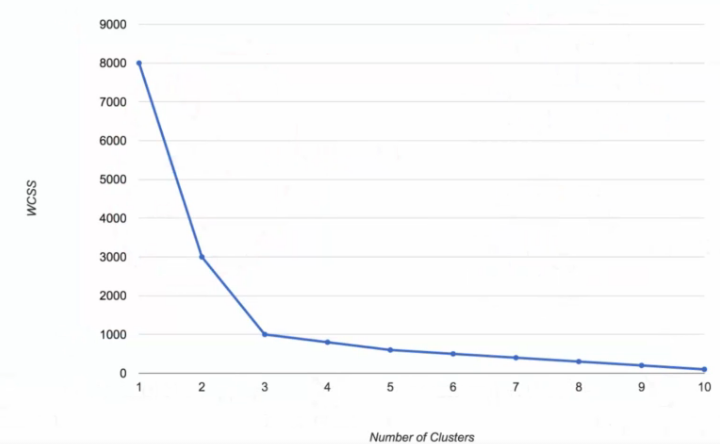
When $K$ is 3, there is no more significant change in WCSS value in the graph. That’s why I pick $K$ as 3.

Example

Code

---

from sklearn.cluster import KMeans

wcss = []

for i in range(1, 11):
    kmeans = KMeans(n_clusters=i, init='k-means++', random_state=42)
    kmeans.fit(X)
    wcss.append(kmeans.inertia_)

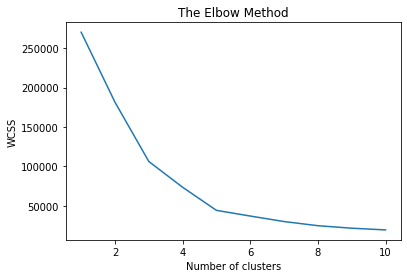
As you can see, when $K$ is 5, there is no significant change in WCSS value.
So, I set $K$ to 5 and implemented it.

kmeans = KMeans(n_clusters=5, init='k-means++', random_state=42)
y_kmeans = kmeans.fit_predict(X)

Result

---

Implementation

• K-Means Clustering
  
• K-Means Clustering & Histograms