What is LDA?
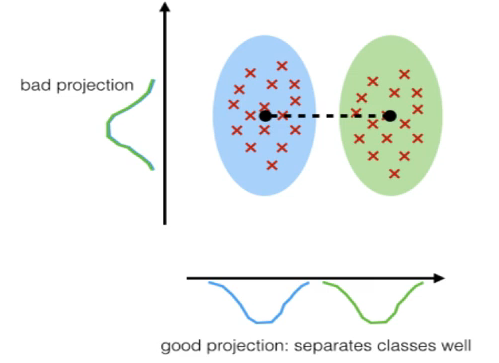
LDA differs from PCA because, in addition to finding the component axises with LDA we are interested in the axes that maximize the separation between multiple classes. PCA is an unsupervised algorithm, while LDA is a supervised algorithm.
LDA is used for:
- Dimensionality reduction
- Pre-processing step for pattern classification
The goal of LDA is:
- Project a dataset a feature space onto a small subspace while maintaing the class discriminatory information.
The role of LDA is:
- Compute the $d$-dimensional mean vectors for the different classes from the dataset.
- Compute the scatter matrices.
- Compute the eigenvectors and corresponding eigenvalues for the scatter matrices.
- Sort the eigenvectors by decreasing eigenvalues and choose $k$ eigenvectors with the largest eigenvalues to form a $d \times k$ dimensional Matrix $W$
- Use this $d \times k$ eigenvector matrix to trasform the samples onto the new subspace.
This can be summarized by the matrix multiplication: $ Y\ =\ X\ \times\ W$
LDA can be expressed as:
Example
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
from sklearn.linear_model import LogisticRegression
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
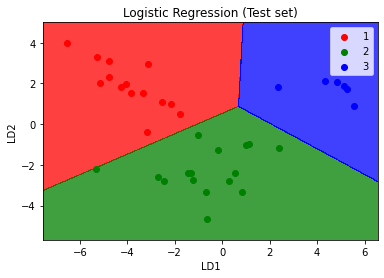
lda = LDA(n_components=2)
X_train = lda.fit_transform(X_train, y_train)
X_test = lda.transform(X_test)
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
Result