What is the Twin Delayed Deep Deterministic Policy Gradient Algorithm (TD3)?
TD3 is a type of deep reinforcement learning. TD3 involves double learning with a single optimal value, which includes two Actor models and four Critic models. Additionally, the policy gradient is used to update the Actor model using the Q-values optimized by the Critic model.
The basic shape of TD3 is:
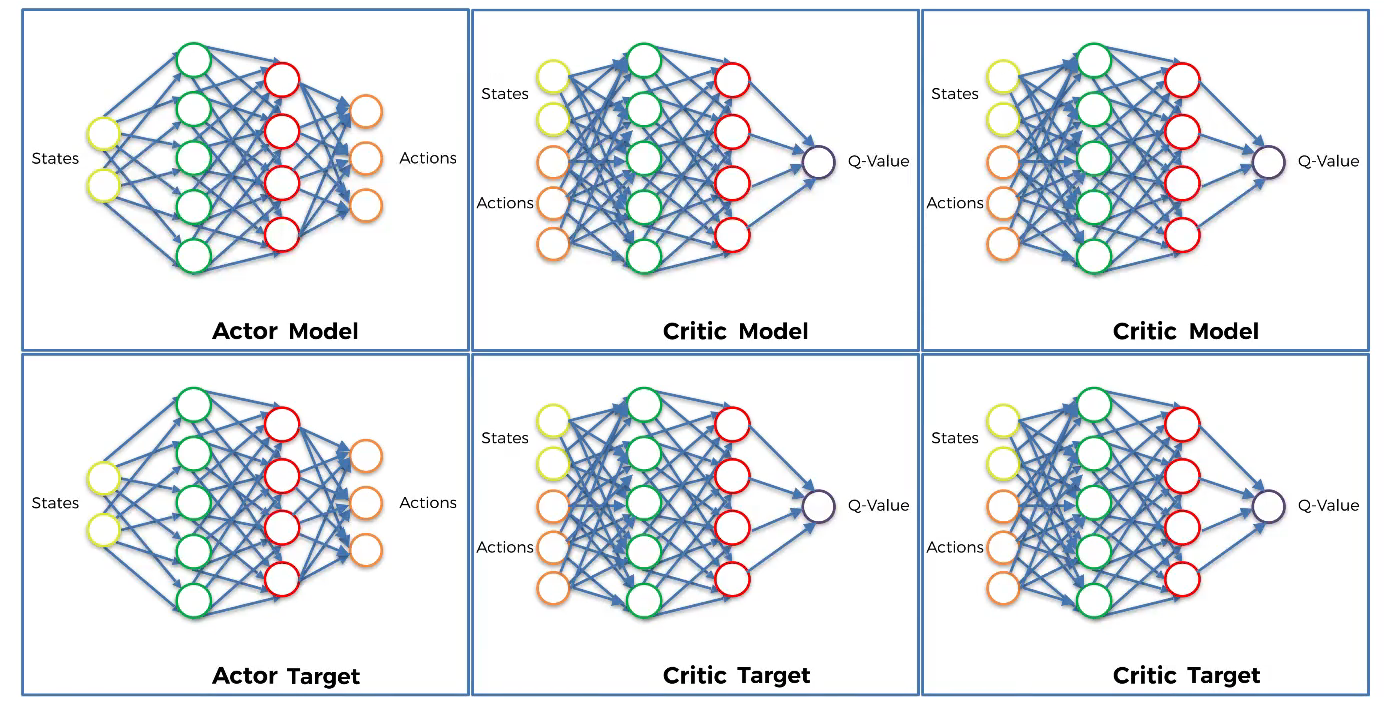
The steps of weight updating are: Actor target → Critic targets → Critic models → Actor model
Steps of TD3
Q Learning part
Initialization
- Step 1
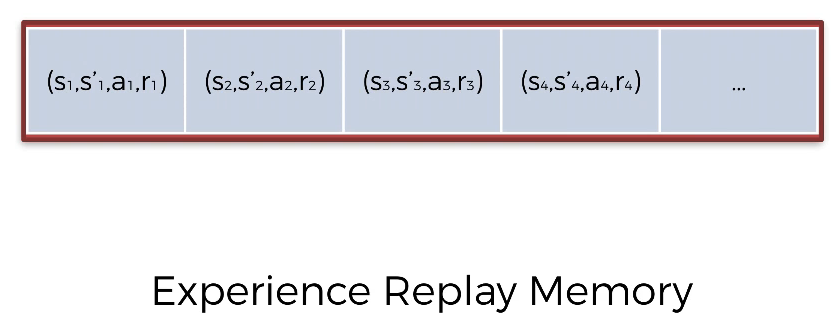
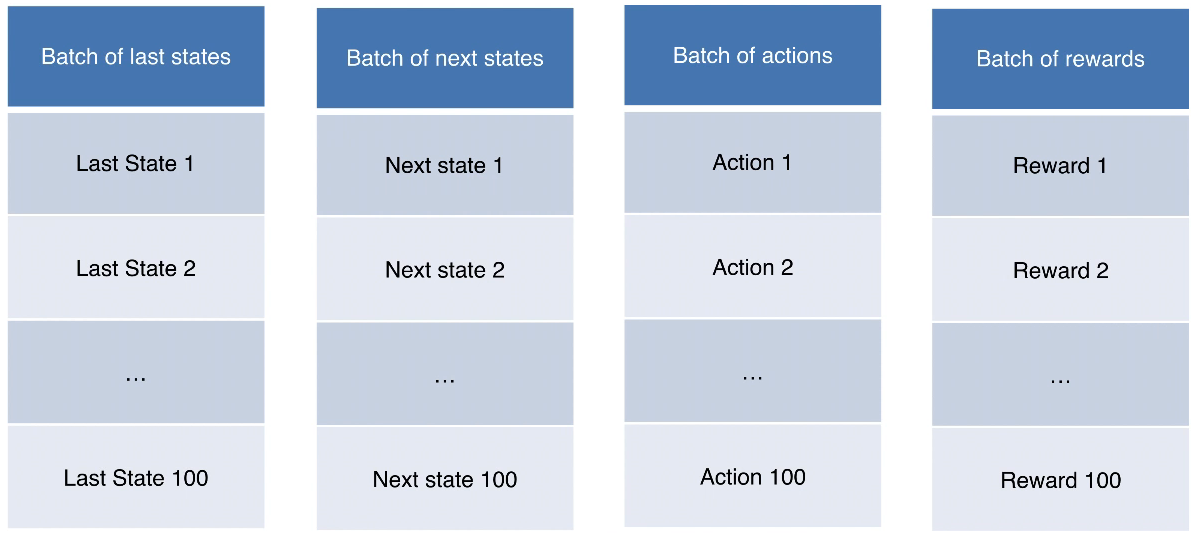
Initialize the Experience Replay Memory that stores past transitions from which we are going to learn our Q-values. The Experience Replay Memory consists of:1 2 3 4
s : current state s' : next state a : action played, it leads s to s' r : reward
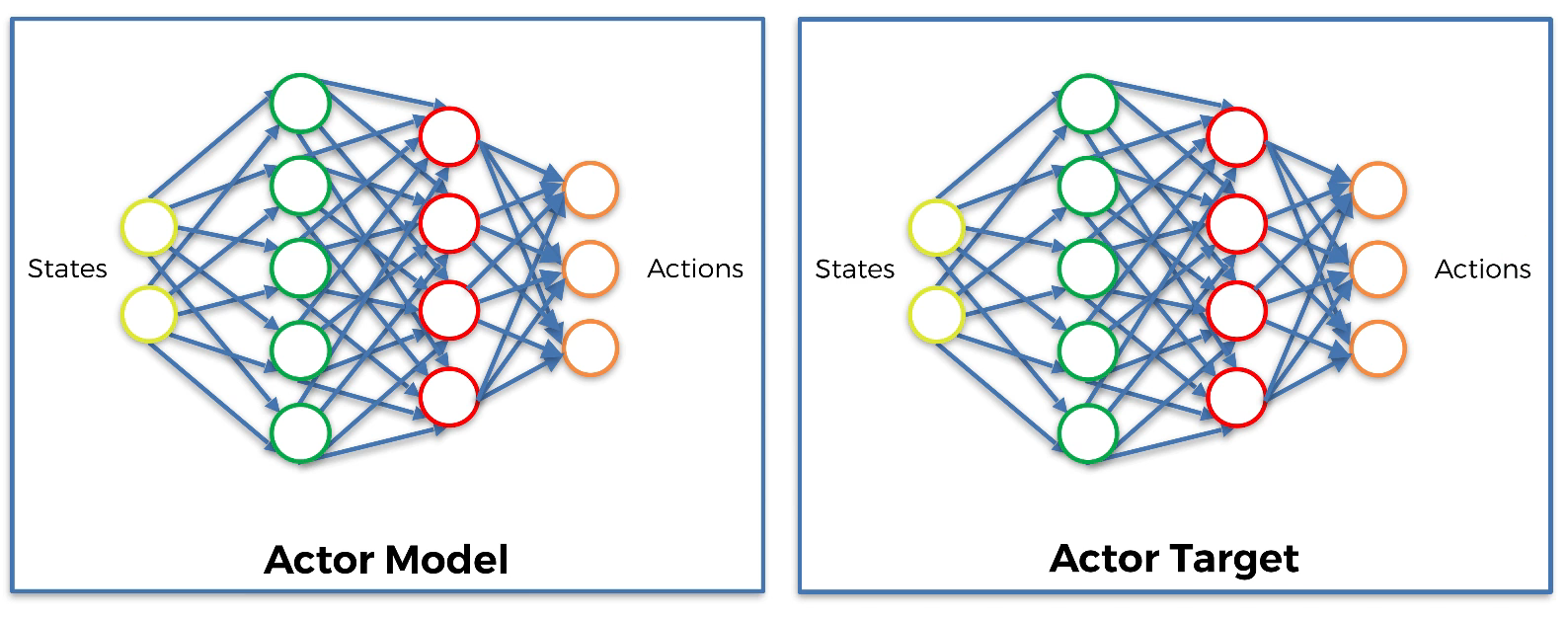
- Step 2
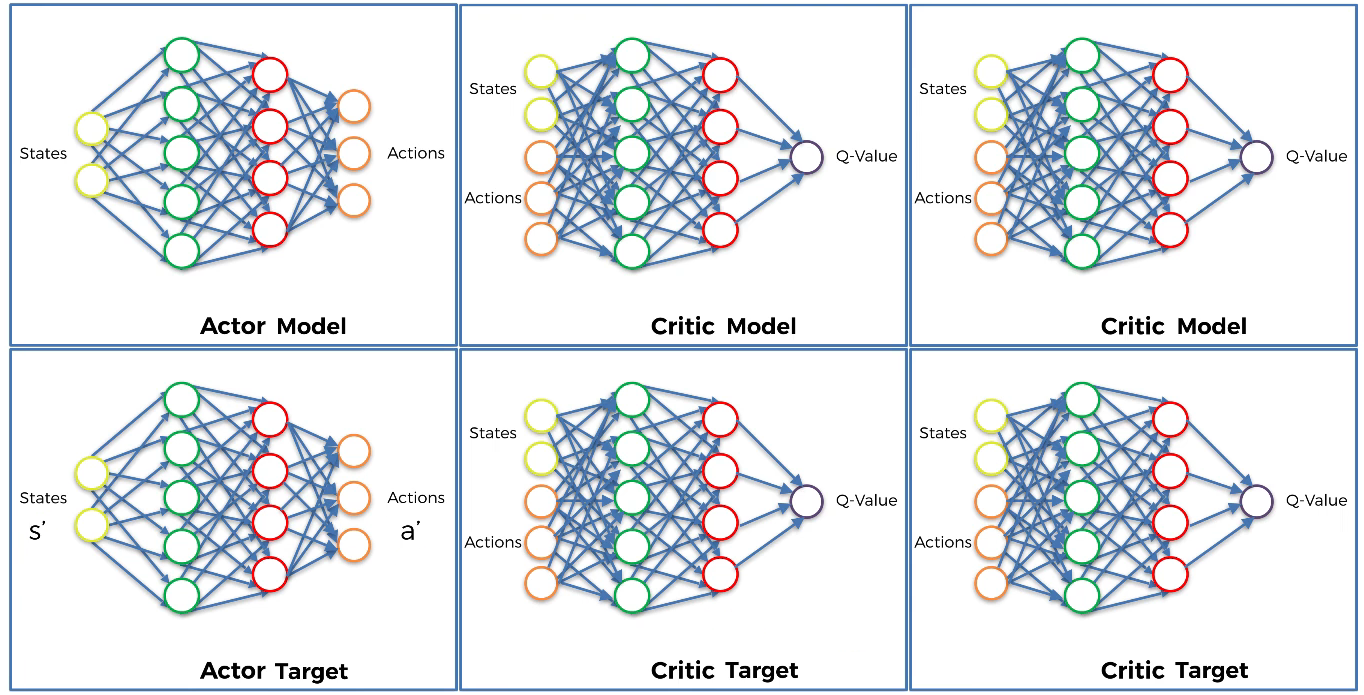
Build one neural network for the Actor model and one neural network for the Actor target.
- Step 3
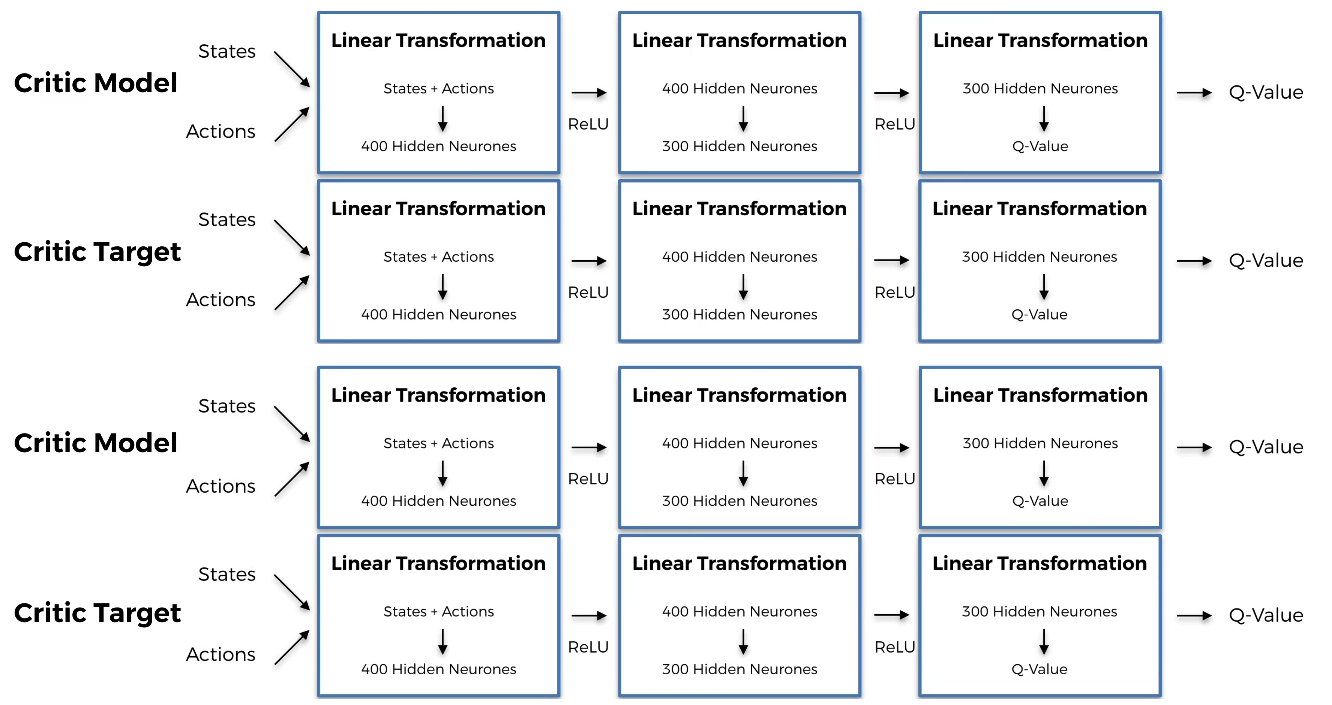
Build two neural networks for the two Critic models and two neural networks for the two Critic targets.
Training process
“Run a full episode with a certain number of actions randomly to avoid ending up in a bad state. And then with actions played by the Actor model. Then repeat the following steps:
- Step 4
Sample a batch of transitions $(s, s’, a, r)$ from the experience replay memory. Then for each element of the batch:
- Step 5
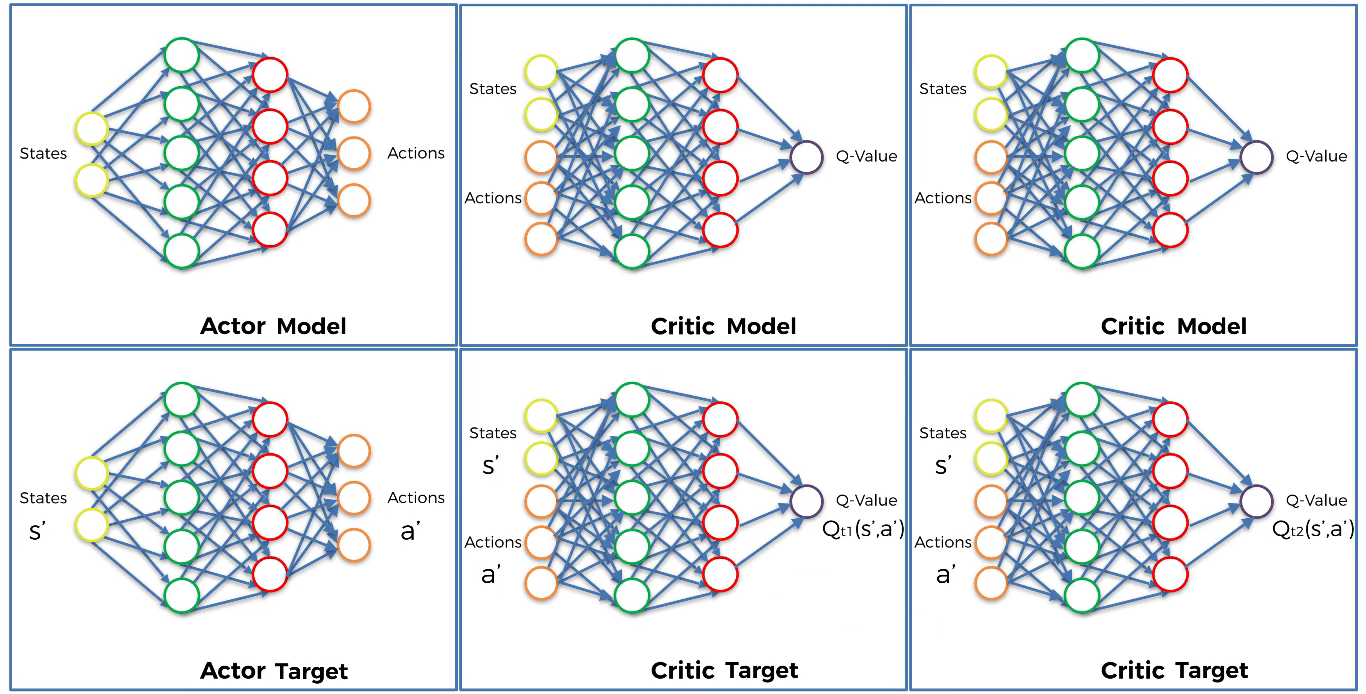
From the next state $s’$ the Actor target plays the next action $a’$.
- Step 6
Add gaussian noise to next action $a’$ and clamp it in a range of values supported by the environment in order to make two actions different. This process will get us better state or avoid the agent from being stuck in a state.
And the formula of gaussian noise is:
$ \tilde{a}\ \gets\ clip(\tilde{a}) $
- Step 7
The two Critic targets each take the pair $(s’, a’)$ as input and return two Q-values $Q_{t1}(s’,a’) $ and $Q_{t2}(s’,a’) $ as output.
- Step 8
Keep the minimum of two Q-values($min(Q_{t1},\ Q_{t2})$) to prevent too optimistic estimates of that value of state. That is, it helps to stabilize the training process.
It represents the approximated value of the next state.
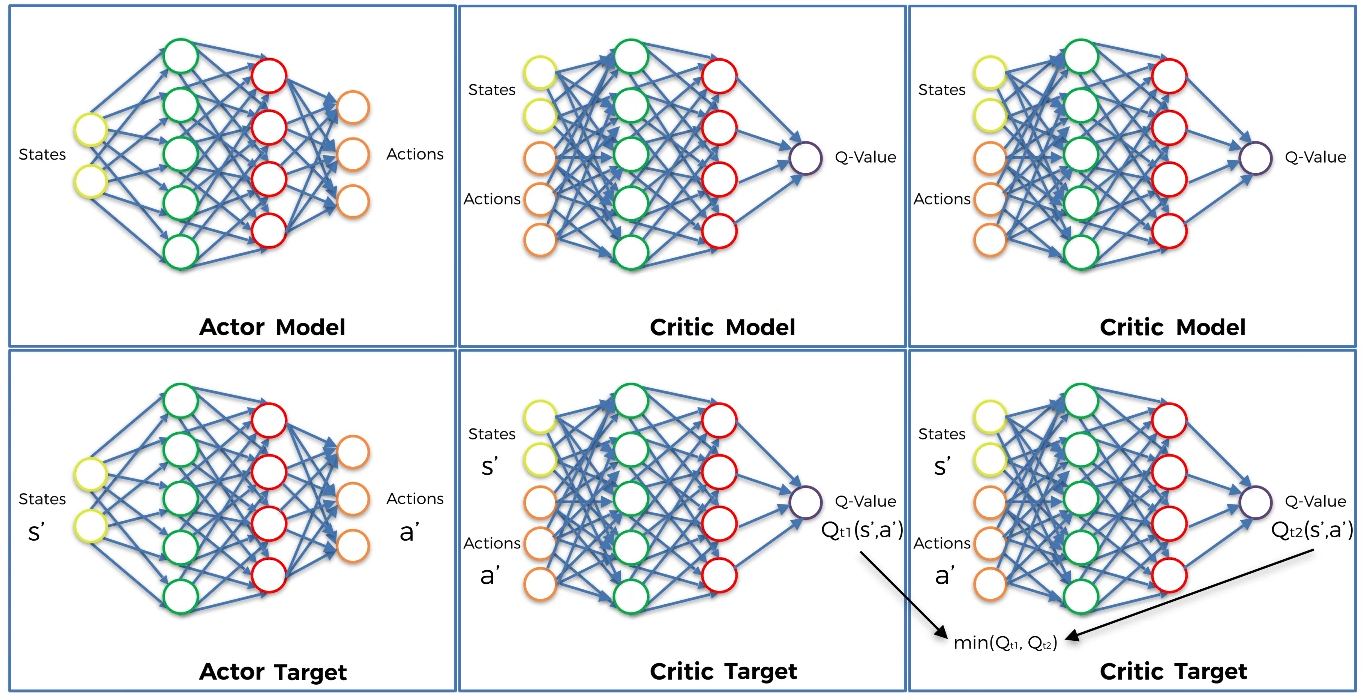
- Step 9
Get the final target of the two Critic models which is:
$Q_{t}\ =\ r\ +\ \gamma\ \times \ min(Q_{t1},Q_{t2})$, where $\gamma$ is the discount factor.
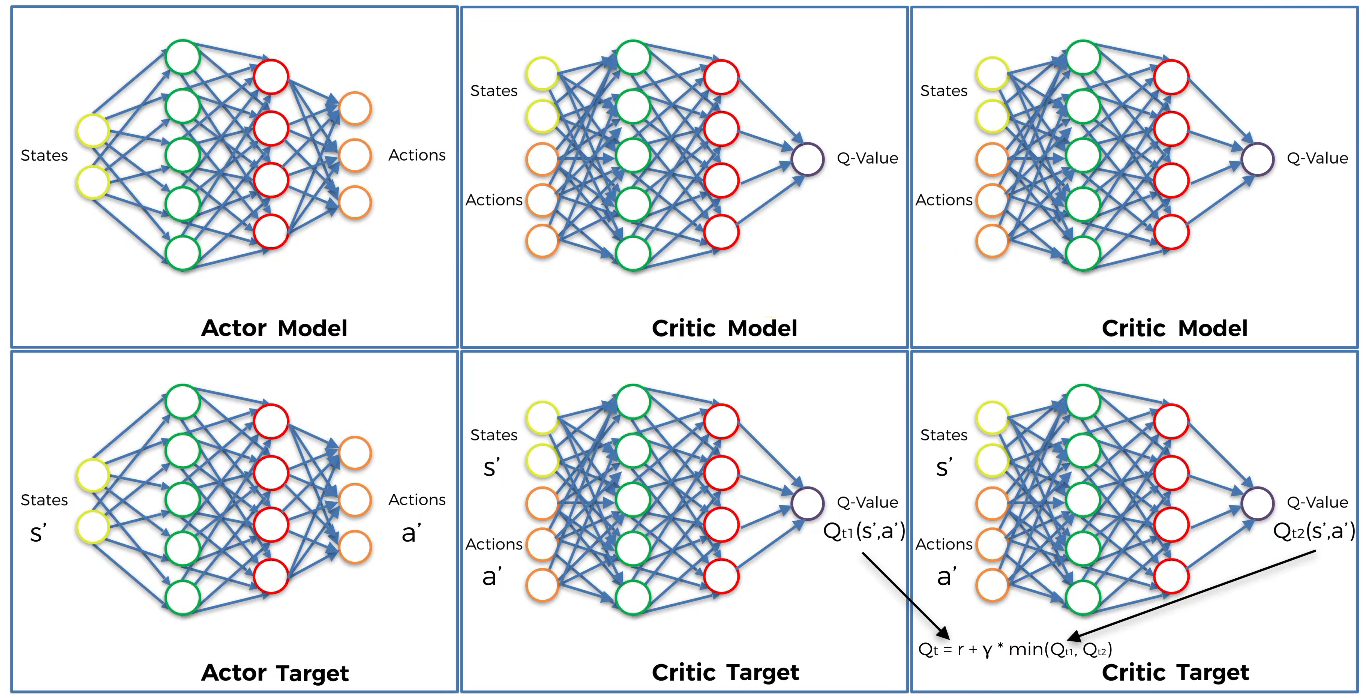
- Step 10
The two Critic models take each the couple(s,a) as input and return two Q-values $ Q_{1}(s,a)$ and $Q_{2}(s,a)$ as outputs.
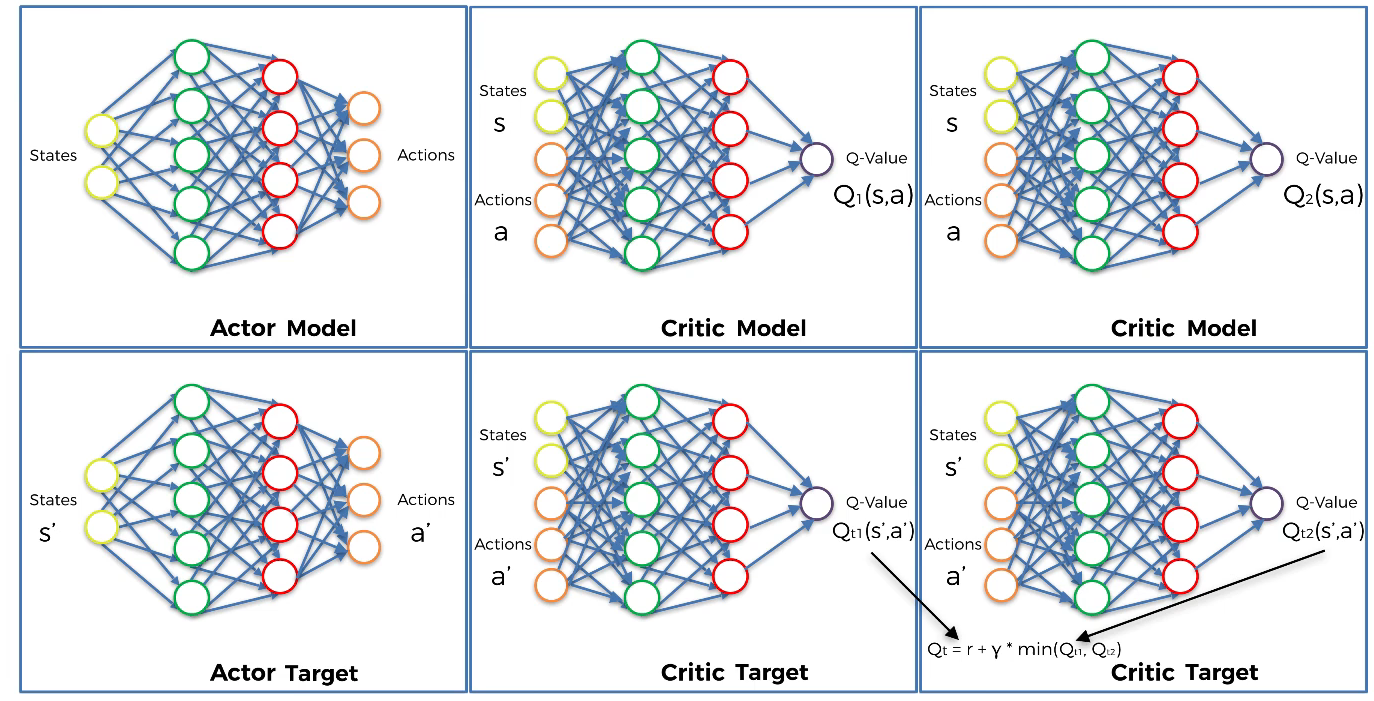
- Step 11
Compute the loss from the two Critic models:
Critic Loss = MSE_Loss $(Q_{1}(s,a),\ Q_{t})$ + MSE_Loss $(Q_{2}(s,a),\ Q_{t})$
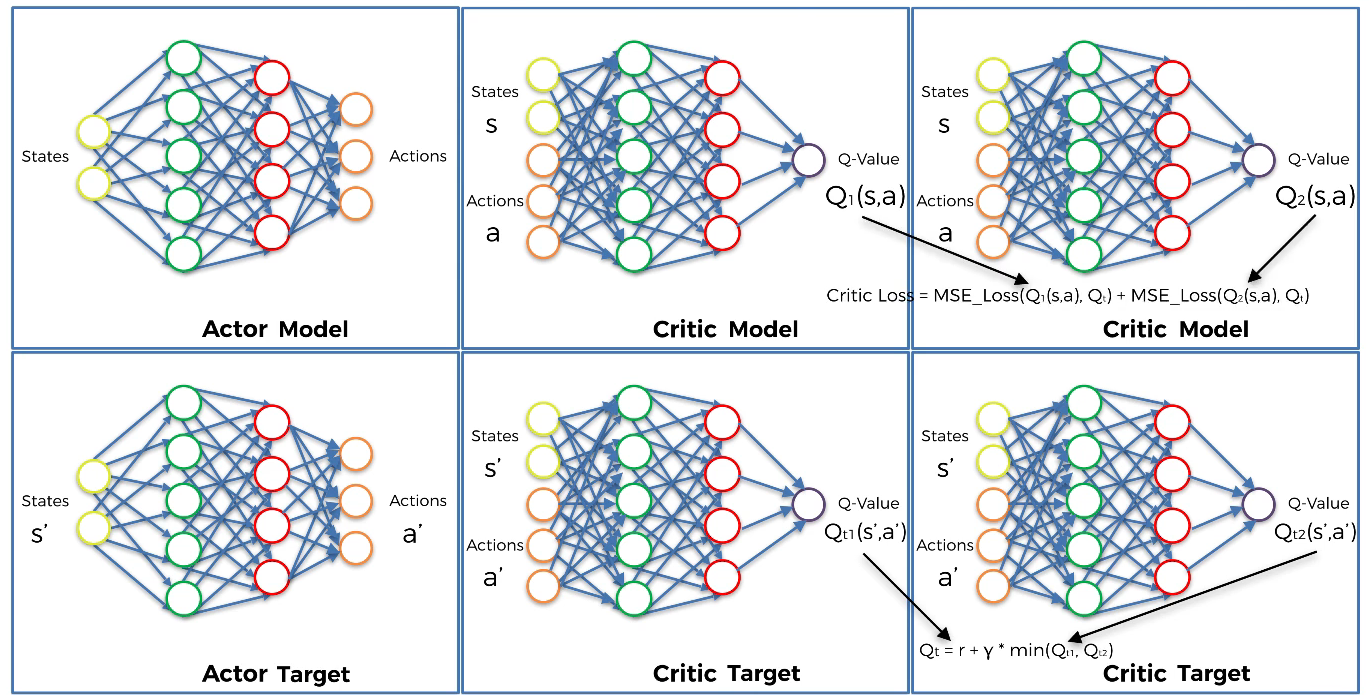
- Step 12
Backpropagate the critic loss and update the parameters of the two Critic models with an SGD optimizer.
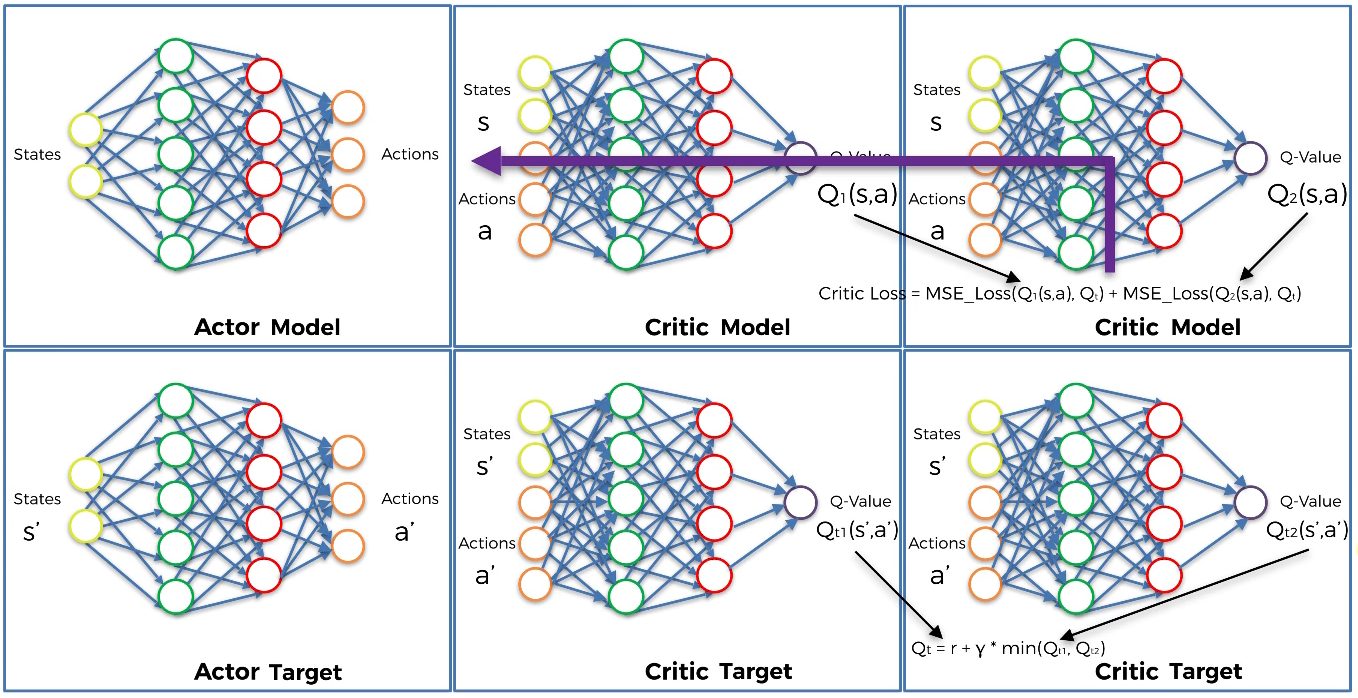
Policy Leraning part
- Step 13
Once every two iterations, update our Actor model by performing gradient ascent on the output of the first Critic model because we want to maximize the Q-value:
$\nabla_{\phi}J(\phi)\ =\ N^{-1}\sum\nabla_{a}Q_{\theta_{1}}(s,a)|{a=\pi{\phi}(s)}\ \nabla_{\phi}\pi_{\phi}(s)$ where $\phi$ and $\theta_{1}$ are resp. the weights of the Actor model and Critic model.
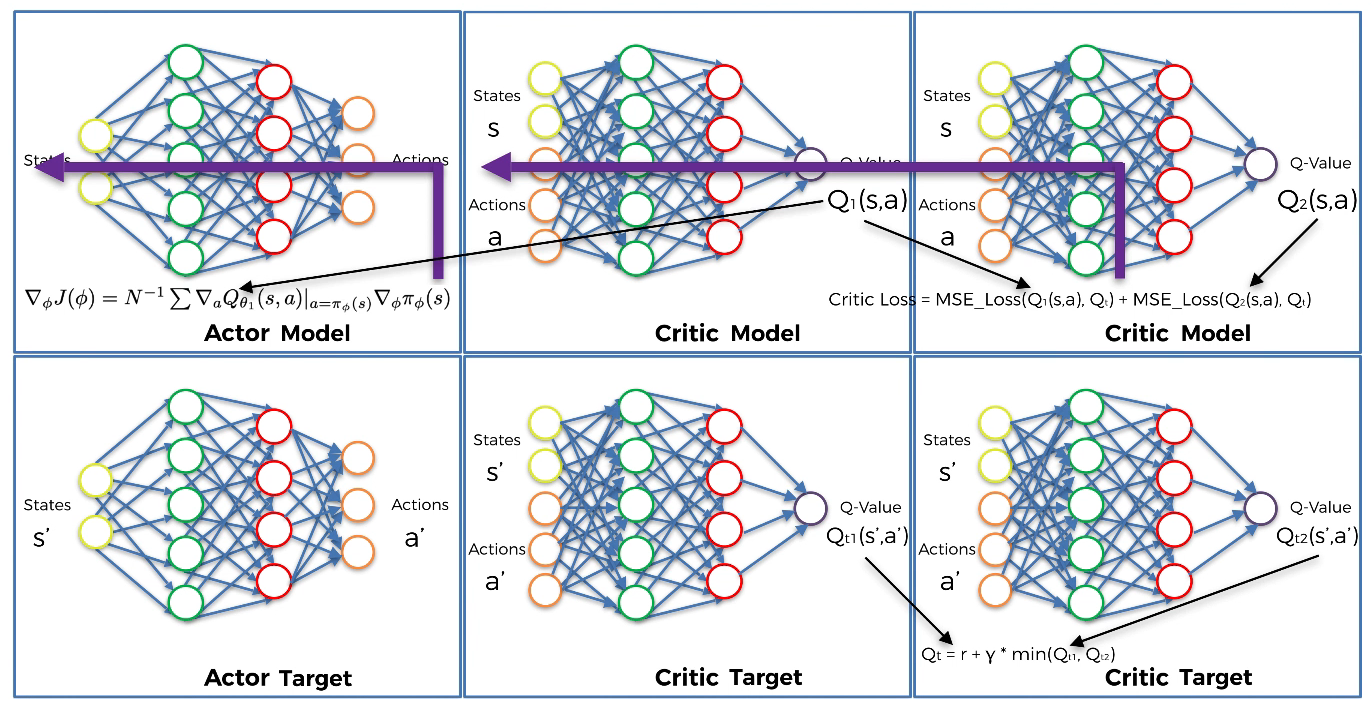
- Step 14
Also, once every two iterations, update the weights of the Actor target by polyak averaging:
$\theta’{i}\ \leftarrow\ \tau\theta{i}\ +\ (1\ -\ \tau\theta’_{i})$ where $\theta$ is the parameter of Actor model and $\theta’$ is the parameter of Actor target. Since $\tau$ is a very small number, the Actor model will slightly transferred its weight to the Actor target.
That is, the Actor target get closer and closer to the Actor model.
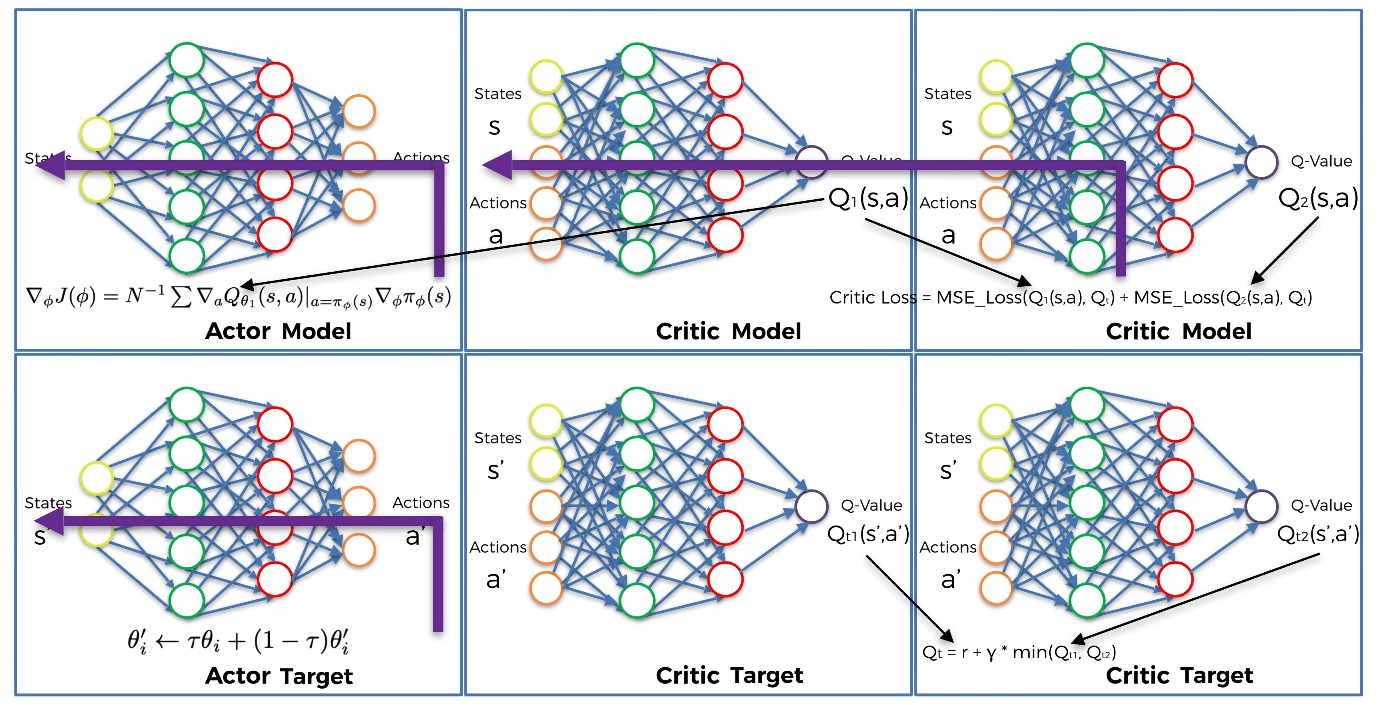
- Step 15
Still once every two iterations, update the weights of the Actor target by polyak averaging:
$\phi’{i}\ \leftarrow\ \tau\phi{i}\ +\ (1\ -\ \tau\phi’_{i})$ where $\phi$ is the parameter of Critic model and $\phi’$ is the parameter of Critic target.
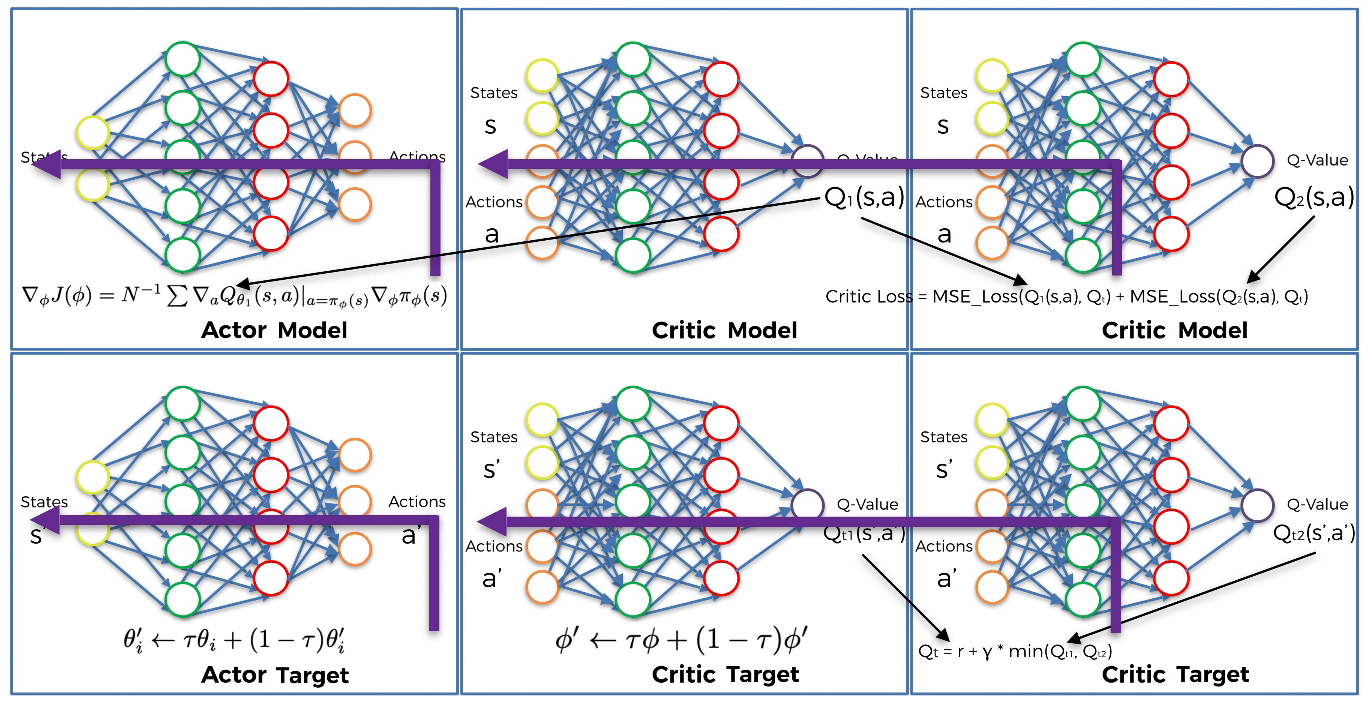
Since updates are made once every two iterations, TD3 includes the word “delay”.
Exmaple
Code
Import libraries
1
2
3
4
5
6
7
8
9
10
11
12
13
import os
import time
import random
import numpy as np
import matplotlib.pyplot as plt
import pybullet_envs
import gym
import torch
import torch.nn as nn
import torch.nn.functional as F
from gym import wrappers
from torch.autograd import Variable
from collections import deque
Step 1. Initialize the Experience Replay memory
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class ReplayBuffer(object):
def __init__(self, max_size=1e6):
self.storage = []
self.max_size = max_size
self.ptr = 0
def add(self, transition):
if len(self.storage) == self.max_size:
self.storage[int(self.ptr)] = transition
self.ptr = (self.ptr + 1) % self.max_size
else:
self.storage.append(transition)
def sample(self, batch_size):
ind = np.random.randint(0, len(self.storage), size=batch_size)
batch_states, batch_next_states, batch_actions, batch_rewards, batch_dones = [], [], [], [], []
for i in ind:
state, next_state, action, reward, done = self.storage[i]
batch_states.append(np.array(state, copy=False))
batch_next_states.append(np.array(next_state, copy=False))
batch_actions.append(np.array(action, copy=False))
batch_rewards.append(np.array(reward, copy=False))
batch_dones.append(np.array(done, copy=False))
return np.array(batch_states), np.array(batch_next_states), np.array(batch_actions), np.array(batch_rewards).reshape(-1, 1), np.array(batch_dones).reshape(-1, 1)
Step 2. Build one neural network for the Actor model and one neural network for the Actor target
1
2
3
4
5
6
7
8
9
10
11
12
13
14
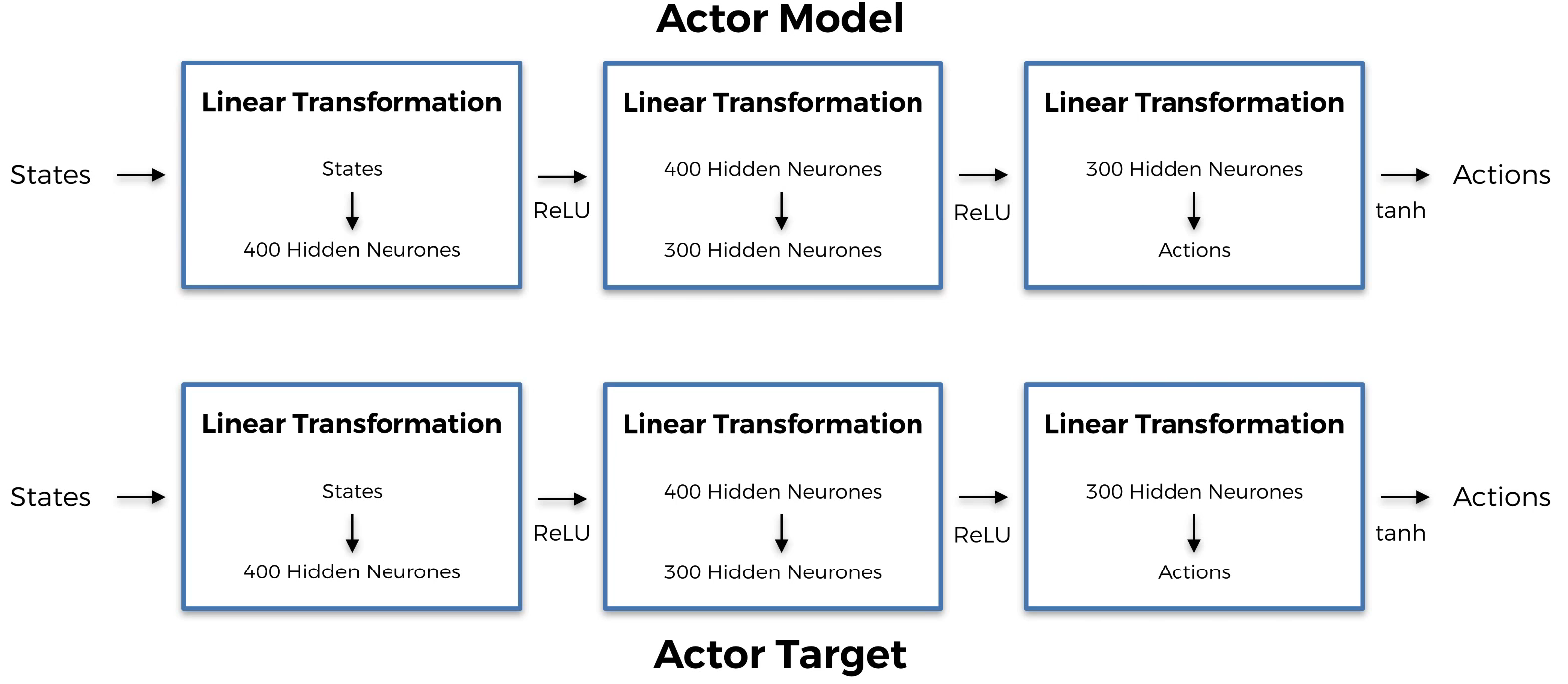
class Actor(nn.Module):
def __init__(self, state_dim, action_dim, max_action):
super(Actor, self).__init__()
self.layer_1 = nn.Linear(state_dim, 400)
self.layer_2 = nn.Linear(400, 300)
self.layer_3 = nn.Linear(300, action_dim)
self.max_action = max_action
def forward(self, x):
x = F.relu(self.layer_1(x))
x = F.relu(self.layer_2(x))
x = self.max_action * torch.tanh(self.layer_3(x))
return x
Step 3. Build two neural networks for the two Critic models and two neural networks for the two Critic targets
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Critic(nn.Module):
def __init__(self, state_dim, action_dim):
super(Critic, self).__init__()
# Defining the first Critic neural network
self.layer_1 = nn.Linear(state_dim + action_dim, 400)
self.layer_2 = nn.Linear(400, 300)
self.layer_3 = nn.Linear(300, 1)
# Defining the second Critic neural network
self.layer_4 = nn.Linear(state_dim + action_dim, 400)
self.layer_5 = nn.Linear(400, 300)
self.layer_6 = nn.Linear(300, 1)
def forward(self, x, u):
xu = torch.cat([x, u], 1)
# Forward-Propagation on the first Critic Neural Network
x1 = F.relu(self.layer_1(xu))
x1 = F.relu(self.layer_2(x1))
x1 = self.layer_3(x1)
# Forward-Propagation on the second Critic Neural Network
x2 = F.relu(self.layer_4(xu))
x2 = F.relu(self.layer_5(x2))
x2 = self.layer_6(x2)
return x1, x2
def Q1(self, x, u):
xu = torch.cat([x, u], 1)
x1 = F.relu(self.layer_1(xu))
x1 = F.relu(self.layer_2(x1))
x1 = self.layer_3(x1)
return x1
Steps 4 to 15. Training Process
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
# Selecting the device (CPU or GPU)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# Building the whole Training Process into a class
class TD3(object):
def __init__(self, state_dim, action_dim, max_action):
self.actor = Actor(state_dim, action_dim, max_action).to(device)
self.actor_target = Actor(state_dim, action_dim, max_action).to(device)
self.actor_target.load_state_dict(self.actor.state_dict())
self.actor_optimizer = torch.optim.Adam(self.actor.parameters())
self.critic = Critic(state_dim, action_dim).to(device)
self.critic_target = Critic(state_dim, action_dim).to(device)
self.critic_target.load_state_dict(self.critic.state_dict())
self.critic_optimizer = torch.optim.Adam(self.critic.parameters())
self.max_action = max_action
def select_action(self, state):
state = torch.Tensor(state.reshape(1, -1)).to(device)
return self.actor(state).cpu().data.numpy().flatten()
def train(self, replay_buffer, iterations, batch_size=100, discount=0.99, tau=0.005, policy_noise=0.2, noise_clip=0.5, policy_freq=2):
for it in range(iterations):
# Step 4: Sample a batch of transitions (s, s’, a, r) from the memory
batch_states, batch_next_states, batch_actions, batch_rewards, batch_dones = replay_buffer.sample(batch_size)
state = torch.Tensor(batch_states).to(device)
next_state = torch.Tensor(batch_next_states).to(device)
action = torch.Tensor(batch_actions).to(device)
reward = torch.Tensor(batch_rewards).to(device)
done = torch.Tensor(batch_dones).to(device)
# Step 5: From the next state s’, the Actor target plays the next action a’
next_action = self.actor_target(next_state)
# Step 6: Add Gaussian noise to this next action a’ and we clamp it in a range of values supported by the environment
noise = torch.Tensor(batch_actions).data.normal_(0, policy_noise).to(device)
noise = noise.clamp(-noise_clip, noise_clip)
next_action = (next_action + noise).clamp(-self.max_action, self.max_action)
# Step 7: The two Critic targets take each the couple (s’, a’) as input and return two Q-values Qt1(s’,a’) and Qt2(s’,a’) as outputs
target_Q1, target_Q2 = self.critic_target(next_state, next_action)
# Step 8: Keep the minimum of these two Q-values: min(Qt1, Qt2)
target_Q = torch.min(target_Q1, target_Q2)
# Step 9: Get the final target of the two Critic models, which is: Qt = r + γ * min(Qt1, Qt2), where γ is the discount factor
target_Q = reward + ((1 - done) * discount * target_Q).detach()
# Step 10: The two Critic models take each the couple (s, a) as input and return two Q-values Q1(s,a) and Q2(s,a) as outputs
current_Q1, current_Q2 = self.critic(state, action)
# Step 11: Compute the loss coming from the two Critic models: Critic Loss = MSE_Loss(Q1(s,a), Qt) + MSE_Loss(Q2(s,a), Qt)
critic_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)
# Step 12: Backpropagate this Critic loss and update the parameters of the two Critic models with a SGD optimizer
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
# Step 13: Once every two iterations, update our Actor model by performing gradient ascent on the output of the first Critic model
if it % policy_freq == 0:
actor_loss = -self.critic.Q1(state, self.actor(state)).mean()
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# Step 14: Still once every two iterations, update the weights of the Actor target by polyak averaging
for param, target_param in zip(self.actor.parameters(), self.actor_target.parameters()):
target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)
# Step 15: Still once every two iterations, update the weights of the Critic target by polyak averaging
for param, target_param in zip(self.critic.parameters(), self.critic_target.parameters()):
target_param.data.copy_(tau * param.data + (1 - tau) * target_param.data)
# Making a save method to save a trained model
def save(self, filename, directory):
torch.save(self.actor.state_dict(), '%s/%s_actor.pth' % (directory, filename))
torch.save(self.critic.state_dict(), '%s/%s_critic.pth' % (directory, filename))
# Making a load method to load a pre-trained model
def load(self, filename, directory):
self.actor.load_state_dict(torch.load('%s/%s_actor.pth' % (directory, filename)))
self.critic.load_state_dict(torch.load('%s/%s_critic.pth' % (directory, filename)))
Make a function that evaluates the policy by calculating its average reward over 10 episodes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def evaluate_policy(policy, eval_episodes=10):
avg_reward = 0.
for _ in range(eval_episodes):
obs = env.reset()
done = False
while not done:
action = policy.select_action(np.array(obs))
obs, reward, done, _ = env.step(action)
avg_reward += reward
avg_reward /= eval_episodes
print ("---------------------------------------")
print ("Average Reward over the Evaluation Step: %f" % (avg_reward))
print ("---------------------------------------")
return avg_reward
Set the parameters
1
2
3
4
5
6
7
8
9
10
11
12
13
env_name = "Walker2DBulletEnv-v0" # Name of a environment (set it to any Continous environment you want)
seed = 0 # Random seed number
start_timesteps = 1e4 # Number of iterations/timesteps before which the model randomly chooses an action, and after which it starts to use the policy network
eval_freq = 5e3 # How often the evaluation step is performed (after how many timesteps)
max_timesteps = 5e5 # Total number of iterations/timesteps
save_models = True # Boolean checker whether or not to save the pre-trained model
expl_noise = 0.1 # Exploration noise - STD value of exploration Gaussian noise
batch_size = 100 # Size of the batch
discount = 0.99 # Discount factor gamma, used in the calculation of the total discounted reward
tau = 0.005 # Target network update rate
policy_noise = 0.2 # STD of Gaussian noise added to the actions for the exploration purposes
noise_clip = 0.5 # Maximum value of the Gaussian noise added to the actions (policy)
policy_freq = 2 # Number of iterations to wait before the policy network (Actor model) is updated
Create a folder
1
2
3
4
5
file_name = "%s_%s_%s" % ("TD3", env_name, str(seed))
if not os.path.exists("./results"):
os.makedirs("./results")
if save_models and not os.path.exists("./pytorch_models"):
os.makedirs("./pytorch_models")
Create the PyBullet environment
1
env = gym.make(env_name)
Set seeds and we get the necessary information on the states and actions in the chosen environment
1
2
3
4
5
6
env.seed(seed)
torch.manual_seed(seed)
np.random.seed(seed)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.shape[0]
max_action = float(env.action_space.high[0])
Create the policy network (the Actor model)
1
policy = TD3(state_dim, action_dim, max_action)
Create the Experience Replay memory
1
replay_buffer = ReplayBuffer()
Define a list where all the evaluation results over 10 episodes are stored
1
evaluations = [evaluate_policy(policy)]
Initialize the variables
1
2
3
4
5
total_timesteps = 0
timesteps_since_eval = 0
episode_num = 0
done = True
t0 = time.time()
Training
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
# Start the main loop over 500,000 timesteps
while total_timesteps < max_timesteps:
# If the episode is done
if done:
# If we are not at the very beginning, we start the training process of the model
if total_timesteps != 0:
print("Total Timesteps: {} Episode Num: {} Reward: {}".format(total_timesteps, episode_num, episode_reward))
policy.train(replay_buffer, episode_timesteps, batch_size, discount, tau, policy_noise, noise_clip, policy_freq)
# Evaluate the episode and we save the policy
if timesteps_since_eval >= eval_freq:
timesteps_since_eval %= eval_freq
evaluations.append(evaluate_policy(policy))
policy.save(file_name, directory="./pytorch_models")
np.save("./results/%s" % (file_name), evaluations)
# When the training step is done, Reset the state of the environment
obs = env.reset()
# Set the Done to False
done = False
# Set rewards and episode timesteps to zero
episode_reward = 0
episode_timesteps = 0
episode_num += 1
# Before 10000 timesteps, play random actions
if total_timesteps < start_timesteps:
action = env.action_space.sample()
else: # After 10000 timesteps, switch to the model
action = policy.select_action(np.array(obs))
# If the explore_noise parameter is not 0, add noise to the action and clip it
if expl_noise != 0:
action = (action + np.random.normal(0, expl_noise, size=env.action_space.shape[0])).clip(env.action_space.low, env.action_space.high)
# The agent performs the action in the environment, then reaches the next state and receives the reward
new_obs, reward, done, _ = env.step(action)
# Check if the episode is done
done_bool = 0 if episode_timesteps + 1 == env._max_episode_steps else float(done)
# Increase the total reward
episode_reward += reward
# Store the new transition into the Experience Replay memory (ReplayBuffer)
replay_buffer.add((obs, new_obs, action, reward, done_bool))
# Update the state, the episode timestep, the total timesteps, and the timesteps since the evaluation of the policy
obs = new_obs
episode_timesteps += 1
total_timesteps += 1
timesteps_since_eval += 1
# Add the last policy evaluation to our list of evaluations and we save our model
evaluations.append(evaluate_policy(policy))
if save_models: policy.save("%s" % (file_name), directory="./pytorch_models")
np.save("./results/%s" % (file_name), evaluations)